cos²(x)+sin²(x)=1

En trigonométrie, il existe une formule très importante qui indique que si x est un angle quelconque, alors cos²(x)+sin²(x)=1. Cette formule est très importante, car elle permet de faire des déductions d’informations non données par un énoncé.

Exemple : Soit x un angle tel que cos(x)=0,8. Que vaut sin(x)?

\\cos^2(x)+sin^2(x)=1
\\⇔0,8^2+sin^2(x)=1
\\⇔0,64+sin^2(x)=1
\\⇔sin^2(x)=1-0,64
\\⇔sin^2(x)=0,36
\\⇔sin(x)=\sqrt{0,36}~ou~-\sqrt{0,36} 
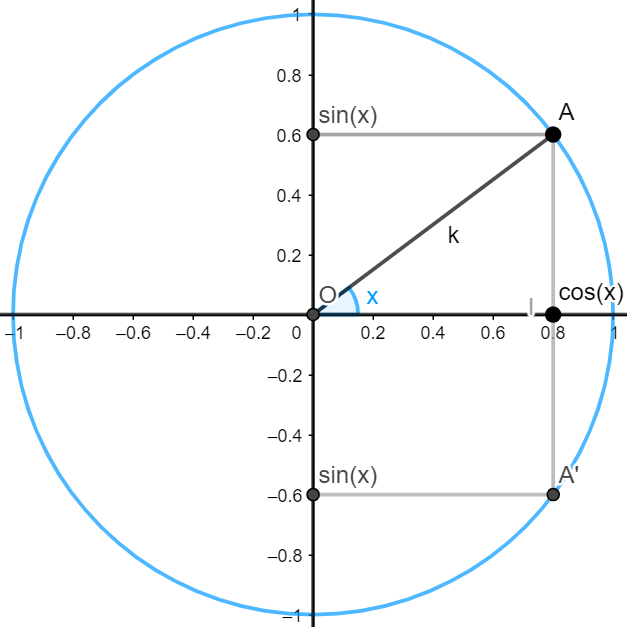
\\⇔sin(x)=0,6~ou~-0,6

Le résultat peut être vérifié graphiquement. Ainsi, si vous vous rappelez que le cosinus d’un angle se lit sur l’axe des abscisses et le sinus sur l’axe des ordonnées, alors on constate que pour une abscisse (donc un cosinus) de 0,8 correspondent deux points: A (dont l’ordonnée, le sinus, vaut 0,6) et A’ (dont l’ordonnée, donc le sinus, vaut -0,6).

Donc cos(x)=0,8 ⇒ sin(x)=0,6 ou sin(x)=-0,6

Mais l’exemple ne fait pas la preuve. Comment démontrer que la formule précédemment évoquée est vraie pour tout réel x (avec x∈ℝ )? C’est ce que nous allons voir maintenant :

Démonstration: Pourquoi cos²(x)+sin²(x)=1

Étape n°1: Faire une figure

Soit~(0;\vec{i};\vec{j})~un~repère~orthonormé.
\\Soit~C~un~cercle~de~centre~O~et~de~rayon~r=1.
\\Soit~M~un~point~quelconque~du~cercle~trigonométrique~tel~que~(\vec{OI}~ ;\vec{OM})=x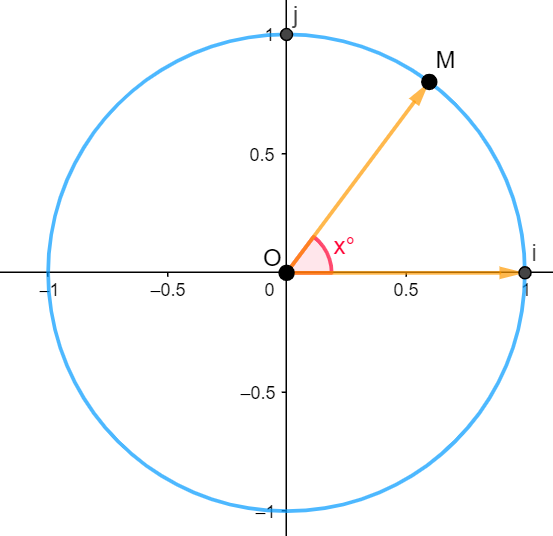

Notons~H~le~pied~de~la~hauteur~issue~de~M

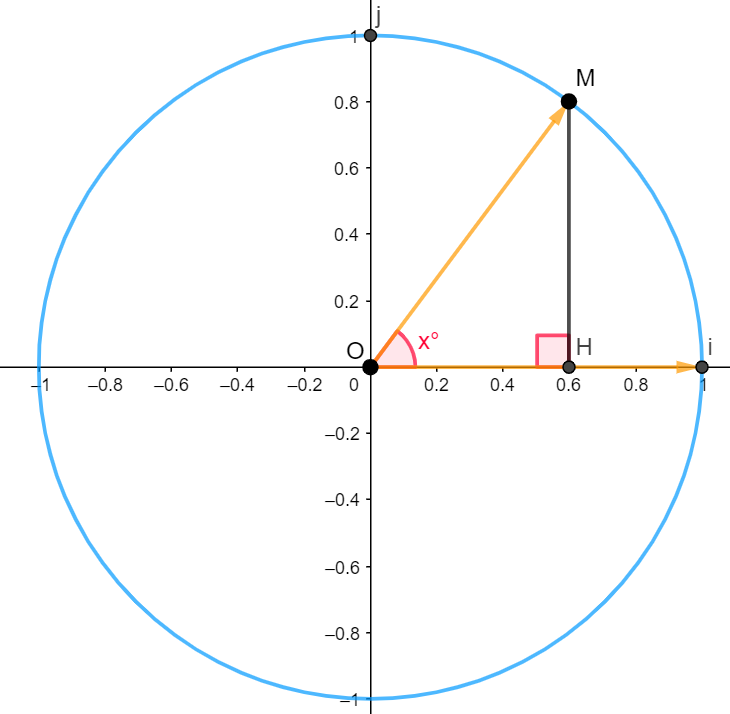
Étape n°2: Utiliser le théorème de Pythagore

Le~triangle~OMH~est~rectangle~en~H.~D'après~le~théorème~de~Pythagore:
\\OH^2+HM^2=OM^2
\\⇔OH^2+HM^2=1^2
\\⇔OH^2+HM^2=1
\\~
\\En~effet,~OM~étant~un~rayon~du~cercle~trigonométrique,~on~a~OM=1

Étape n°3: Utiliser les formules de trigonométrie du collège

\\On~le~voit,~on~vient~de~faire~apparaître~une~équation~dont~le~carré~de~deux~membres~vaut~1.~\\Cela~ressemble~à~la~formule~que~l'on~cherche~à~démontrer~:cos^2(x)+sin^2(x)=1
\\Mais~comment~aller~plus~loin?
\\~
\\~Faisons~un~bond~en~arrière~en~classe~de~3ème.~
\\ Rappel~de~collège~(trigonométrie):~SOH~CAH~TOA
\\~
\\Cela~signifie~que~sin(x)=\frac{(côté)~opposé}{hypoténuse}~~;~~cos(x)=\frac{(côté)~adjacent}{hypoténuse}~~;~~tan(x)=\frac{(côté)~opposé}{(côté)~adjacent}
\\~
\\Dans~notre~cercle~trigonométrique,~on~a~:
\\~
\\sin(x)=\frac{opposé}{hypoténuse}=\frac{HM}{OM}=\frac{HM}{1}=HM~(car~OM=r=1)
\\~
\\cos(x)=\frac{adjacent}{hypoténuse}=\frac{OH}{OM}=\frac{OH}{1}=OH
\\~
\\~Nous~avons~le~droit~de~remplacer~OH~par~cos(x),~car~OH=cos(x). 
\\~De~même,~nous~avons~le~droit~de~remplacer~HM~par~sin(x)~car~HM=sin(x).

Étape n°4: On finit l’équation

OH^2+HM^2=1~(voir~étape~n°2). 
\\Or,~OH=cos(x)~et~HM=sin(x)~(voir~étape~n°3)
\\~
\\En~remplaçant~OH~par~cos(x),~et~HM~par~sin(x),~on~trouve:
\\~
\\{\color{blue} OH}^2+{\color{orange}HM}^2=1
\\⇔{\color{blue}cos}^2{\color{blue}(x)}+{\color{orange}sin}^2{\color{orange}(x)}=1.
\\~
\\La~formule~est~démontrée.

Note pour les élèves de niveau avancé: On l’a vu, dans le cadre d’un cercle trigonométrique de rayon 1, cos²(x)+sin²(x)=1. Mais que ce serait-il passé si le rayon du cercle ≠ 1? La formule resterait néanmoins vraie (voir l’explication).

Conclusion

Comme vous le voyez, la démonstration n’est pas facile. Ne cherchez pas à l’apprendre par cœur, essayez plutôt de comprendre la logique derrière.

Essayez de comprendre comment, en combinant une représentation graphique (le dessin) et en réutilisant plusieurs concepts de base (théorème de Pythagore, trigonométrie), vous pouvez prouver quelque chose de beaucoup plus avancé qui permet de déduire une information manquante (calculer cos en fonction de sin).

Cela n’est pas facile. Peut-être devrez vous relire le raisonnement à plusieurs reprises avant de bien le comprendre. Mais ce n’est pas grave. C’est en réfléchissant et en comprenant (plutôt qu’en apprenant par cœur) que vous développerez votre agilité, votre intelligence mathématique, votre créativité et votre curiosité qui seront nécessaires en première et en terminal,e lorsque vous aurez des problèmes de plus en plus complexes à résoudre. Certes, apprendre par cœur est souvent utile, mais avant d’apprendre, tâchez de comprendre.

Cet article est désormais terminé. J’espère qu’il vous a plu et bonne visite sur BossdesMaths.com