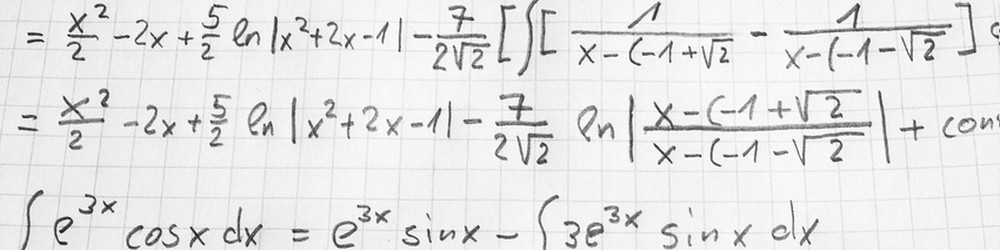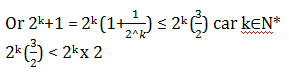Obtenir de bonnes notes en mathématiques n’est pas toujours facile. En effet, connaître les propriétés de votre cours ne suffit pas. Encore faut-il comprendre le langage mathématique, notamment les différentes questions du problème pour savoir ce qu’on attend de vous et déterminer quels outils vous permettront de répondre à la question. Or, il est facile de se perdre entre les symboles grecs (α, β, ∀, ∈, ∉, Δ, ∫, A ∩ B, Un, f’…), les termes techniques (« montrer que », « prouver que », « déduire », « si et seulement si ») et les questions à rallonge.
Tout comme l’anglais, l’espagnol ou l’allemand, les mathématiques sont une langue. Donc savoir traduire un énoncé français en équation mathématique ou réciproquement (traduire un énoncé mathématique en langue française) est la clé pour résoudre les problèmes mathématiques. Par conséquent, si vous avez envie d’obtenir de bonnes notes au bac, vous devrez donc apprendre à maîtriser le langage mathématique.
Mots clés à connaître (Langage mathématique)
Déduire
Déduire signifie « Se baser sur les questions précédentes pour répondre à une question ». Si vous ne savez pas où aller, alors relisez les questions précédentes, l’énoncé, la figure (s’il y en a une) et demandez-vous quelle information est la plus susceptible de vous aider pour répondre à la question.
En savoir plus : Je suis perdu : que faire ?
Exemplef(x) = 3x²+2x+6, g(x) = 2x²+x+1, f et g sont toutes deux définies dans ℝ • Question a : Montrer que f(x)-g(x) = x²+x+5 • Question b : En déduire que f(x) > g(x) Question a On met déjà les fonctions entre parenthèses pour ne pas faire d’erreur de signe f(x)-g(x) = (3x²+2x+6)-(2x²+x+1) = 3x²+2x+6-2x²-x-1 = x²+x+5 Question b On sait que f(x)-g(x) = x²+x+5 (question a). Calculons le discriminant (Δ) de x²+x+5 Δ = b²-4ac= 1²-4(1)(5) = 1 – 20 = -19 Δ<0, x²+8x+4 est toujours du signe de a, donc positif Donc ∀x∈ℝ, x²+8x+4>0 ⇒ ∀x∈ℝ, f(x)-g(x) > 0 ⇒ ∀x∈ℝ, f(x) > g(x) |
Montrer par récurrence
Montrer par récurrence implique de prouver que la propriété est vraie au rang n = 0. Puis il faut montrer que si la propriété est vraie au rang n, alors elle est vraie au rang n+1 (principe d’hérédité).
ExempleU1 = 1 Un+1 = 2Un+1 Prouver que pour ∀k∈ℕ*, Uk≤2k Étape 1: pour k = 1 U1 = 1 21 = 2 La propriété est vraie au rang k=1 Étape 2: supposons qu’au rang k∈ℕ* (k≥2), Uk ≤2k. Montrons que Uk+1 ≤2k+1 On sait que Uk+1 = 2Uk+1 Or Uk≤2k par hypothèse de récurrence Donc 2Uk+1 ≤ 2k+1 Donc Uk+1 ≤ 2k+1 (car Uk+1 = 2Uk+1)
Donc 2k+1 ≤ 2k+1 (2k+1 = 2k x 2) Donc Uk+1 ≤ 2k+1 ≤ 2k+1 L’hypothèse de récurrence est vérifiée. On peut donc affirmer que pour ∀k∈ℕ*, Uk ≤2k |
Prouver que
En mathématiques, il faut toujours prouver ses dires (dire le triangle est rectangle, ça se voit = pas bon). Voici deux exemples : vie de tous les jours et langage mathématique.
Les mathématiques ne sont pas si dures que cela. Il faut juste formaliser votre raisonnement. Voici les étapes clés :
Note: Dans certains problèmes simples, l’étape 2 peut être « sautée » mais c’est rare. Les étapes 1 et 3 ne doivent JAMAIS être sautées. |
Montrer par l’absurde
Montrer par l’absurde signifie prouver le contraire de ce que l’on veut prouver jusqu’à aboutir à un résultat aberrant, ce qui prouve que l’hypothèse initiale est exacte.

Quelques termes techniques
∀ : Ce symbole signifie « pour tout »
∈ : Cela signifie appartient
∉ : Ce symbole signifie n’appartient pas
Δ : Permet de calculer le discriminant d’une fonction du second degré.
f'(x) désigne la dérivée de la fonction
f’ ‘(x) désigne la dérivée seconde.
SSI Ce terme signifie « SI et seulement SI »
F(x) désigne une des primitives de la fonction f(x).
A ∩ B : Signifie l’intersection de l’ensemble A et B (A et B)
A U B : Désigne la probabilité de A ou de B.
En savoir plus : Table de symboles mathématiques
Les ensembles

En savoir plus sur les ensembles
3 conseils pour améliorer durablement vos notes
Vous avez compris l’énoncé mathématique ? Ne vous ruez pas pour autant sur votre calculatrice. Un problème mathématique ne commence JAMAIS par un calcul. Donc, avant de commencer un exercice, demandez-vous ce qu’on attend de vous (ce qu’il faut montrer, où il faut aller) puis déterminez quelles sont les ressources à votre disposition.
Voici trois autres « tips » qui peuvent vous aider :
- Même si ce n’est pas indiqué, faites une figure quand vous le pouvez car cela peut vous aider à stimuler votre intuition.
- Si vous ne savez pas où aller, alors relisez dans votre livre les différentes propriétés du chapitre en cours. Demandez-vous lesquelles semblent le plus utile.
- Vous ne savez toujours pas où aller? essayez de simplifier votre calcul (les mathématiques = simplification) en tentant une factorisation ou, si cela ne fonctionne pas, un développement de votre expression algébrique.
Lire aussi :
Besoin d’aide en mathématiques ?
Vous avez des questions, vous souhaitez bénéficier de cours particuliers ou participer à l’un des stages Boss des Maths ? N’hésitez pas à nous contacter en utilisant le formulaire ci-dessous. Bonne journée à vous et bonnes révisions 😃🏋️💪🎓!