Beaucoup de gens pensent que les mathématiques ne servent à rien au quotidien et ne sont que des faits abstraits qu’on peut oublier dès qu’on sort de l’école. Beaucoup de gens pensent que les mathématiques sont inutiles. Et vous?
❌ C’est faux. En effet, les mathématiques semblent invisibles car elles sont… partout. Et elles peuvent être fort amusantes ou divertissantes. Voici quelques fun facts sur les mathématiques
Fun fact n°1: Pythagore n’a pas inventé son théorème
Ce n’est pas Pythagore qui a découvert le célèbre théorème… qui était déjà connu des Chinois et des Egyptiens 1000 ans plus tôt. Mais cela a été le premier a le démontrer… C’est ainsi qu’il serait rentré dans la postérité… Mais ce n’est pas tout…
Fun fact n°2: Notre Dame de Paris a été construite grâce au fait que 3²+4²=5²
C’est sur cette base que les maçons auraient construit de grands monuments (pyramides d’Egypte ou Notre Dame de Paris). Ils utilisaient une corde a 13 nœuds qui une fois tendue respectait les proportions 3-4-5. Ne restait plus qu’a construire les murs le long des 2 côtés adjacents à l’angle droit et on avait un bel angle droit.

C’est grâce à la corde à 13 nœuds que les architectes du château de Guédelon (un château fort actuellement en cours de construction, oui en 2023) construisent leur château!
Fun fact n°3: La vraie raison pour laquelle les huîtres sont vendues par 12
Les huîtres sont généralement vendues par 12 car 12 possède plein de facteurs: 1,2,3,4,6,12. Cela simplifie énormément le partage. Cela signifie qu’avec 12 huîtres, on peut
• Table de 12: manger 1 huître chacun (peu mais pourquoi pas)
• Table de 6: 2 huîtres chacun
• Table de 4: 3 huîtres chacun
• Table de 3: 4 huîtres chacun
• Table de 2: 6 huîtres chacun
• Table de 1: 12 huîtres, évidemment
Aucun produit n’est vendu par nombre premier car cela ne facilite pas le partage: 11 huîtres à 2: soit on fait 5/6 ou 5.5/5.5 mais le 0.5 est crade. Cela ne facilite pas le packaging: 12 bières: pack de 6×2 mais 11 bières? Un carton de 11 de long et 1 de large? pas pratique).
Les mathématiques sont partout 😉
Fun fact n°4: Les fractions, responsables de la réforme des retraites
Le saviez-vous? La cause principale de la réforme des retraite est… une fraction.
Au numérateur : la durée moyenne de la retraite (dépensé publique)
au dénominateur: la durée de cotisation (recette publique).
pour quelqu’un qui travaille a 22 ans part a la retraite a 62 ans et meurt a 82 cette fraction vaut 20/40 soit 1/2 soit une année de retraite pour 2 cotisées.
pour diminuer une fraction (dépenses par rapport aux recettes) on peut soit réduire le numérateur (19/40 < 20/40) soit augmenter le dénominateur (19/41 < 19/40).
C’est exactement ce qu’a voulu faire le gouvernement en passant la retraite a 64 ans. passer de 20/40 a 18/42 en réduisant a la fois le numérateur et en augmentant le dénominateur.
D’1 pierre 2 coups : cela réduit la fraction de 14% donc les dépenses de 14%. impopulaire mais moins que de baisser les retraites de 14% ou d’augmenter les cotisations de 16% (1/0.86=1.16)
Fun fact n°5: Les impôts, à l’origine de l’innovation mathématique
Le saviez-vous? Les ancêtres des calculatrices furent inventées principalement pour faciliter les calculs des percepteurs d’impôts. quand il s’agit de taxer l’Etat est doué en matiere d’innovation…
Petite citation philosophique: L’art de l’imposition consiste à plumer l’oie pour obtenir le plus possible de plumes avec le moins possible de cris [Jean-Baptiste Colbert]
Bien? pas bien? A vous de décider mais une chose est sure: les mathématiques sont partout

Fun fact n°6: Calcul = Caillou
Le saviez vous? Le mot calcul vient du mot » caillou ». Quand les bergers comptaient leurs chèvres ou moutons, ils comptaient avec leurs doigts et quand ils arrivaient a 10 ils mettaient un gros caillou (symbole des dizaines).
Une fois le comptage fini, les unités étaient symbolisées par un petit caillou. ainsi 32 chèvres = 3 gros caillou et 2 petits.
Au retour il suffisait de faire l’inverse (enlever un gros caillou dès que 10 chevres rentraient ou un petit à chaque chèvre) pour voir combien de chèvres manquaient (perdues donc à chercher ou mangées par un prédateur/volées)
C’est en comptant des chèvres pour des raisons de manutention que des gens jamais allés a l’école et utilisant un matériau abondant ( le caillou) ont inventé la base 10 du calcul ainsi que l’addition et la soustraction.
Fun fact n°7: Les Etats sont à l’origine (étymologique) des statistiques
Le saviez-vous ? « Statistiques » vient du mot « State » (Etat). En effet, les entités publiques ont besoin, pour gouverner, de comprendre leurs concitoyens (besoins, attentes) mais aussi pour les besoins des taxes. Mais ceux-ci étant trop nombreux pour être étudiés individuellement, les états ont développé la branche des mathématiques intitulées les statistiques pour étudier les masses.
Conséquence : chaque branche des statistiques est un compromis entre synthèse de l’information et recherche de clareté d’un côté, perte d’information de l’autre.
Exemple : cinq personnes gagnent 1300€ – 1400€ – 1800€ – 2 400€ – 5 100€
Le salaire moyen est de (1300+1400+1800+2400+5100)/5=2400€ (salaire moyen français)
😊 C’est la part théorique d’un partage parfaitement équitable
☹La moyenne est tirée par les valeurs extrêmes et est peu représentative des extrêmes
La médiane est de 1800€ (salaire médian français)
😊 La médiane est peu influencée par les extrêmes et est représentative de ce qui se passe « au milieu ». Elle est plus fiable que la moyenne
☹ La médiane ne dit rien sur les inégalités. Le groupe {200,300,1800,1800,1 000 000} a aussi une médiane de 1800…
L’étendue : Max – Min. Elle est ici de 5100-1300=3800
😊 L’étendue mesure les différences. Pratique pour mesurer les inégalités
☹ Elle n’indique rien sur la répartition ni sur les montants dans l’absolu. Ainsi {1300€ – 1400€ – 1800€ – 2 400€ – 5 100€} et {2300€ – 5400€ – 6000€ – 6 100€ – 6 100€} ont la même étendue bien que cachant des réalités très différentes
Mode, écart-type… chaque outil statistique est une simplification d’une réalité visant à rendre intelligible et à mesurer un phénomène bien précis dans un objectif bien précis. Bref, les nombres ne sont pas neutres, surtout lorsque l’on parle de… « state »istics.
Fun fact n°8: Les abeilles maîtrisent les coordonnées polaires [programme de 1ere]
Le saviez-vous? Les abeilles utilisent grosso modo le programme de trigonométrie de 1ere spécialité mathématique (coordonnées polaires re^iθ) pour communiquer entre elles.
• Elles indiquent la distance (r) entre la ruche et les champs de fleurs en dansant. Une danse rapide signifie une distance faible, une danse lente signifie une distance importante. La modélisation fait penser à une fonction exponentielle décroissante ou une fonction inverse.
• Elles indiquent l’angle (chez les scouts on appelle cela azimut) à suivre par rapport à la direction du soleil afin de permettre aux copines de retrouver la direction des champs de fleurs une fois sorties de la ruche.
Vous pensez que c’est une blague? Et bah non, cette découverte de Karl von Frisch lui a valu un prix Nobel en 1973. Pas mal non?
Autre fun fact: les abeilles forment des ruches en hexagones car c’est le polygone régulier qui maximise l’espace utile (ratio alvéoles/espace total) au sein de la ruche tout en assurance une excellente solidité structurelle. Maximiser l’espace utile de stockage de miel (en minimisant la taille des « murs ») leur permet de stocker plus de miel en utilisant moins de ressources (cire), ce qui augmente leur probabilité de survie à l’issue de l’hiver.
Bref, les mathématiques sont partout…. En savoir plus
Fun fact n°9: Pourquoi les feuilles A4 mesurent 21×29,7 cm
Pourquoi le papier standard mesure 21×29,7 cm (et pas 20×30 cm disons)? Il existe une raison très simple. La voici
Fait: Pour fabriquer des feuilles, les imprimeurs utilisent une grande feuille A0 qu’ils plient en deux pour faire deux feuilles A1, qui une fois pliées et redécoupées donnent 4 feuilles A2 puis 8 feuilles A3 ou 16 feuilles A4… Retenez juste que les formats de feuilles se font par pliage et découpage successif d’une grande feuille… https://lnkd.in/eDitwM6V
Conséquence: Si les feuilles A4 mesuraient 20 x 30 cm, le ratio longueur/largeur vaudrait 30/20=1.5. Mais une fois pliée en deux (pour faire du A5), la nouvelle feuille mesurerait 20×15 cm et la nouveau ratio vaudrait 20/15≈1.33
Problème: Le nouveau ratio serait différent, ce qui signifierait des proportions différentes. Cela obligerait les imprimeurs à devoir réadapter leur impressions (marges différentes) ou à accepter un rendu esthétique différent lorsqu’un document est imprimé sur une feuille plus grande ou plus petite qu’au format A4. Compliqué d’un point de vue graphique et logistique.
Solution: Se baser sur le format 21×29,7 cm.
La raison: Le ratio L/l d’une feuille A4 vaut 29,7/21≈1.41428571429. En réalité, ce ratio vaut √(2)≈1,414213562. Pourquoi c’est plus simple? Car c’est le seul ratio de page qui permet, en pliant une feuille en deux, de conserver le rapport entre longueur et largeur de la feuille. Ainsi, lorsque l’on plie la feuille en 2, la nouvelle feuille mesure 21×14,85 cm et 21/14,85 vaut toujours ≈ 1.41. Ainsi les proportions sont conservées, il suffit d’imprimer plus petit pour avoir le même rendu graphique peu importe la taille de la feuille utilisée (explication plus poussée en image)
Conclusion: C’est grâce aux ratios et à la racine – √(2) – que l’on explique le format des feuilles A4 et qu’on a simplifié le travail des imprimeurs et des designers… Les maths sont partout 😉
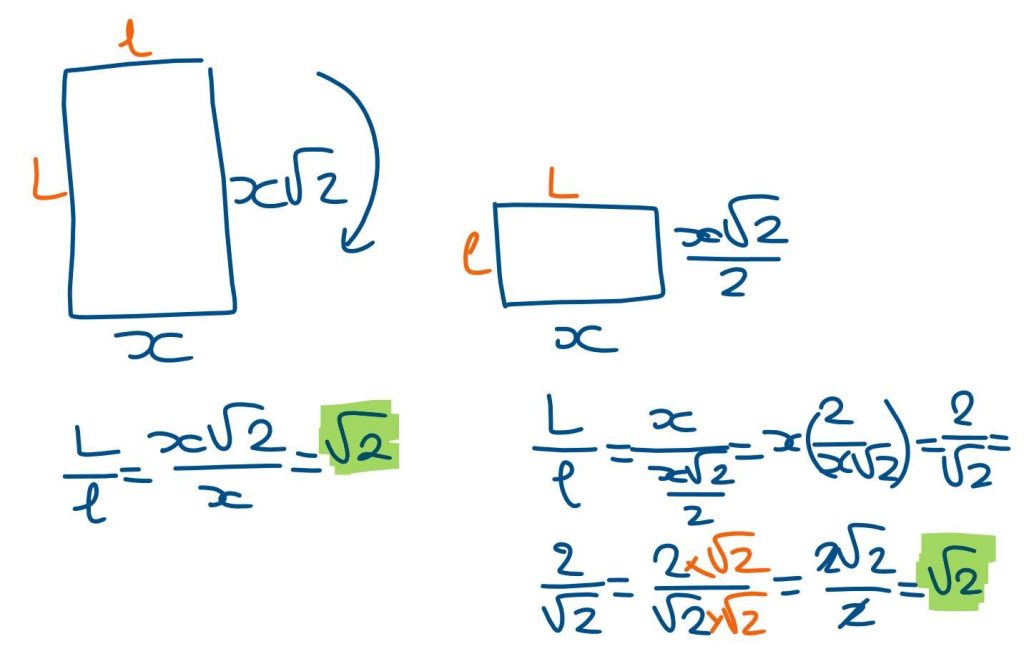
Fun fact n°10= 0.9999999…=1
1=0.9999… (9 écrit une infinité de fois). Etrange non? Pourtant c’est mathématiquement exact. La preuve:
(1/3)=0.33333333…
⇔ 3(1/3)=3×0.33333333…
⇔ 3/3=0.99999999…
⇔ 1=0.99999999…
Ce qu’il fallait démontrer 😮
🐉 Fun fact n°11: Les dragons ne peuvent pas exister 🐉
Fun fact: les dragons n’existent pas et ne peuvent pas exister (du moins pas sur Terre). La preuve par les maths.
Il existe une loi mathématique sympa qui s’appelle k/k²/k^3. Que dit cette loi mathématique?
Si on multiplie par k les dimensions d’un objet alors l’aire sera multipliée par k² et le volume par k au cube. Petite démonstration pratique

Le cube de gauche. Disons qu’il fait 1 cm d’arête.
• Arête = 1 cm
• Aire = 6 faces = 6 cm²
• Volume = 1^3=1 cm^3
Multiplions le par 3. Cela donne un rubik’s cube.
• Arête = 3 cm (petit rubik)
• Aire = 6 faces de 3×3 = 6×9=54 cm²
• Volume = 3^3 = 27 cm^3
En multipliant par 3 la longueur d’une arête, on a multiplié par 9 (3 au carré) l’aire des surfaces extérieures (avant: 6 après 54) et par 3 au cube (27) le volume.
Le rapport avec les dragons? Il est très simple. Prenons un oiseau lambda. Multiplions sa taille par 2 et gardons ses proportions intactes
• Ses ailes, en 2D verront leur surface (donc leur portance) multipliée par 4 (2 au carré)
• Le poids du volatile (qui dépend lui du volume) sera multiplié par 8 (2 au cube)
Bref, en grossissant, la portance des ailes augmente moins vite que le poids de l’animal, rendant le décollage de plus en plus difficile.
Bon la nature est plus maligne que ça
• Les gros oiseaux n’ont pas les mêmes proportions que les petits. Les albatros ont des ailes beaucoup plus longue que les moineaux en proportion
• Les oiseaux ont certains os creux pour diminuer leur masse.
• Les gros oiseaux compensent leur difficulté à décoller en s’aidant de la vitesse qu’ils peuvent atteindre grâce à la gravité (aigles qui se laissent tomber du pic rocheux pour atteindre une vitesse suffisante pour décoller) soit grâce aux pistes de décollage improvisées (les cygnes doivent accélérer et courir sur l’eau pour atteindre la vitesse critique de décollage).
Les avions pour décoller utilisent la même stratégie que le cygne. Ils devraient normalement avoir des ailes de plusieurs km de long pour décoller comme un pigeon. Ils compensent leurs ailes microscopiques (par rapport à leur poids) par une vitesse de décollage élevée (environ 300 km/h).
Le rapport avec les dragons? Pour décoller, un gros dragon devrait avoir soit des ailes de plusieurs centaines de mètres de long, soit un poids plume (dragon fait principalement de vide) soit un dragon surpuissant capable de courir à plusieurs centaines de km/h pour pouvoir décoller. Peu plausible sur Terre. Mais plausible dans une planète avec moins de gravité, donc moins de difficulté à décoller.
Bref, les maths viennent de démontrer pourquoi les dragons ne peuvent exister et pourquoi les oiseaux sont petits 😉
Fun fact n°12: La puissance des intérêts composés
Fun fact: Si Jésus avait déposé 0,01€ sur un livret A rémunéré 3%/an, en l’an 1100, il aurait déjà eu 25 000 milliards d’euros de fortune (0,01*1,03^1200≃25 000 milliards) soit 40 fois plus que Jeff Bezos, Elon Musk et Bernard Arnault réuni. Avec 2%, il n’aurait eu « que » 209 millions en l’an 1200, mais 200 000 milliards en 2024 (plus que le PIB Mondial)
Conclusion 1: Le travail ne rend pas riche. Votre travail apporte un revenu linéaire, vos investissement un revenu exponentiel. Utilisez votre travail comme levier/support sous-jacent à l’investissement (on peut investir plus avec un gros salaire qu’un petit) mais n’économisez pas sous après sous, ça ne sert à rien*.
Conclusion 2: Facile d’être milliardaire si on est immortel ou qu’on gère un patrimoine façon dynastie. Si on ne l’est pas, il faut néanmoins jouer sur le temps long et les intérêts plus que l’investissement initial pour développer un solide patrimoine.
Conclusion 3: Sur le long terme les intérêt composés engendrent une pression incommensurable sur l’environnement car implique une croissance exponentielle de la consommation de matière première.
* La preuve: 60% du patrimoine français est hérité. Dit autrement, naître dans la bonne famille aide plus que tout ce que vous pourrez accomplir de votre vivant (en moyenne). Ca ne veut pas dire qu’il ne faut pas étudier bien sûr mais qu’il vaut mieux comprendre le système qu’être « simplement » un « bon élève ». (Source)
Fun fact n°13: le cercle = forme parfaite
Le cercle est la forme géométrique permettant de maximiser la surface tout en minimisant le périmètre (idem pour la sphère, mais en 3D). C’est pour cette raison que
• Les oiseaux pondent des œufs globalement ronds (bien que légèrement allongés pour des raisons physiologiques) : moins de coquille à produire et plus de volume, donc un bébé plus gros et plus développé, plus apte à la survie. Et moins de risque de casse (pas d’angle).
• Les planètes sont rondes car c’est la forme la plus stable/optimale de la matière en situation de gravité
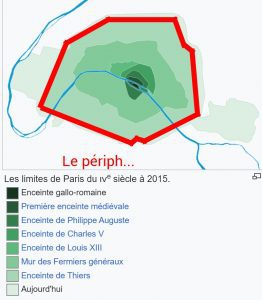
• Les villes fortifiées au moyen-âge étaient globalement circulaire (d’où le périphérique parisien, en forme circulaire, car situé sur une ancienne muraille) car cela permettait de maximiser l’aire (donc le nombre d’habitants protégés à l’intérieur) tout en minimisant le périmètre (donc le coût de construction, de maintenance et de militarisation pour protéger la ville contre les ennemis)
Tout dans la vie vient du cercle ou du 0.
Fun fact n°14: Certains nombres apparaissent plus que d’autres
Question : Y-a-t-il plus de nombres qui commencent par 1, ou par 2, ou par 8 ? A priori, on a envie de dire non… et en fait la réponse est… Oui
Preuve : Lorsque les nombres sont distribués de façon aléatoirement, il y a beaucoup plus de nombres qui commencent par 1 que par 2, par 2 que par 3… Prenons l’exemple des villes de plus de 100 000 habitants en France
• Nombre de villes qui commencent par 9 : 0
• Nombre de villes qui commencent par 8 : 1 (Marseille : 870321)
• Nombre de villes qui commencent par 7 : 0
• Nombre de villes qui commencent par 6 : 0
• Nombre de villes qui commencent par 5 : 1 (Lyon : 522 228)
• Nombre de villes qui commencent par 4 : 1 (Toulouse : 498 003)
• Nombre de villes qui commencent par 3 : 2 (Nice et Nantes)
• Nombre de villes qui commencent par 2 : 6 (Paris : 2 145 906, Montpellier…)
• Nombre de villes qui commencent par 1 : 31
Un hasard ? Non, c’est la même chose en business : il y a plus d’entreprises dont le chiffre d’affaires commence par 1 que par 2, par 2 que par 3…
Etrange non ? Pas tant que ça
Explication : Beaucoup de phénomènes commencent à 0. Avant d’être une grande ville, Lyon était il y a bien longtemps un petit village. Avant de devenir un géant mondial, Apple était une start-up dans un garage… Pour atteindre une grande taille, il faut croitre. Or, la croissance se fait généralement de façon géométrique (1/2/4/8…) pas arithmétique (1/2/3/4…)
Une ville du camp des 1 (exemple : Nancy 104 000 habitants) doit augmenter sa taille de 92% pour rejoindre le camp des 2 (>200 000 hab). Alors que 15% de croissance suffisent pour que Lyon (522 228 habitants) rejoigne le camp des 6. Bref à taux de croissance constant, on reste plus longtemps dans le camp des 1 que dans le camp des 2, le 2 que le 3…
Fun fact : La distribution des clics dans les résultats de Google suit une loi de Benford. Et la loi de Benford est aussi utilisée pour les contrôles fiscaux…Les maths sont partout.
Source: https://fr.wikipedia.org/wiki/Loi_de_Benford, https://fr.wikipedia.org/wiki/Liste_des_communes_de_France_les_plus_peupl%C3%A9es
🧐 Et vous, connaissez-vous d’autres fun facts sur les mathématiques? N’hésitez pas à me le faire savoir en m’envoyant un email ci-dessous
