Vous peinez à déchiffrer les symboles mathématiques? Dans cet article se trouvent les principaux symboles utilisés en mathématiques et ce qu’ils signifient. Bonne lecture.
| Symbole mathématique | Signification en français | Exemple | Ce qu’il faut comprendre |
| ∈ | Appartient | x ∈[2;5] | Pour exprimer une solution ou l’appartenance d’un nombre ou d’une variable à un ensemble |
| ℕ | Entier naturel (0,1,2,3…) | 0,1,2,3… | Soit u(n)=3n+4 une suite définie sur ℕ signifie qu’on peut remplacer n par 0,1,2,3 mais pas par -2 ni 1/2 |
| * | Privé de 0 ℕ* signifie | x∈ ℕ* | Soit x∈ ℕ* … Cela signifie que x peut valoir 1 ou 2 ou 18 ou 1555 mais pas 0 |
| ℤ | Entier (positif ou négatif) | -10;-5;1;2;8 | Soit x∈ℤ signifie que x peut prendre n’importe quelle valeur, du moment qu’il n’y a pas de décimales. |
| ⅅ | Nombre décimal | -0,2, 0.5… | Nombre pouvant être écrit (nombre fini de décimale) |
| ℚ | Ensemble des nombres pouvant être écrits sous forme d’un quotient mais pas forcément sous forme décimale | 2/3 ; -1/2; 2 (car 2=4/2) ou -10 | |
| ℝ | Ensemble des nombres réels | 2,3,π | Soit x∈ℝ |
| \ | Privé de | ℝ\{2;3} | Tous les réels sauf 2 et 3 |
| ℂ | Ensemble des nombres complexes | 3+2i 2-i | Déterminer les solutions de l’équation z²+2z+10 (z∈ℂ) |
| | | Tel que | Soit n∈ℕ | n>10 | n est un entier strictement supérieur à 10. n∈]10;+∞[ |
| ∀ | Pour tout | ∀x∈ℝ | ∀x∈ℝ, ex>0 |
| ∃ | Il existe | ∃x∈ℝ | |
| ∉ | N’appartient pas | 0∉[2;5] | |
| ⊂ | Inclus | ℕ⊂ℝ | L’ensemble des entiers (ℕ) fait partie des réels (ℝ) mais certains réels (comme π ou -3) ne sont pas des entiers. ℕ est un sous-ensemble de ℝ Le symbole inclus concerne les intervalles |
| ⊄ | Non-inclus | ||
| Ø | Ensemble vide | S={Ø} signifie qu’il n’existe pas de solution | |
| ∫ | Intégrale | ||
| ⇒ | Implique | x>2 ⇒ x²>4 | Désigne une déduction à sens unique x>2⇒x²>4 signifie Si x>2 alors x²>4 (ce qui est vrai) Attention: dans l’autre sens ce n’est pas vrai x²>4 ne signifie pas que x>2 (x peut aussi valoir -10…) |
| ⇔ | Equivalent | x3=8⇔x=2 | Ce symbole signifie à la fois ⇒ et ⇐ x3=8⇒x=2 (si x3=8 alors x=2) x3=8⇐x=2 (si x=2 alors x3=8) |
| ∩ | Inter | p(A∩B) | En probabilité, cela signifie que l’évènement A et B sont réalisés en même temps. |
| ∪ | Union | ||
| ∞ | Infini | ||
| Lim | Limites | Les limites signifient les tendances à long terme. ici cela signifie que plus x deviendra grand, plus l’image de f sera grande (et finira par dépasser n’importe quel réel) | |
| [ ] | Modulo | 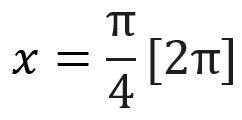 | Cela signifie qu’on peut ajouter un certain nombre de fois le nombre écrit entre crochet. Ici x peut valoir π/4 mais aussi π/4 + 2π ou π/4 – 2π Ce symbole s’utilise en trigonométrique ou en physique pour les phénomènes périodiques (ondes…) |
| ⊥ | Perpendiculaire | (AB)⊥(AC) | |
| > | Supérieur | x>3 | x doit valoir une valeur supérieure à 3 (3 exclus). Cela est équivalent à dire x∈]3, +∞[ |
| < | Inférieur | x<3 | x doit valoir une valeur inférieure à 3 (3 exclus). Cela est équivalent à dire x∈]-∞;3[ |
| ⩾ | Supérieur ou égal | x⩾3 | x peut valoir au moins 3 (3 inclus). Cela est équivalent à dire x∈[3;+∞[ |
| ⩽ | Inférieur ou égal | x⩽3 | x peut valoir au plus 3 (3 inclus). Cela est équivalent à dire x∈]-∞;3] |
| i | Nombre complexe | Définition: i²=-1 Exemple: -4=4(-1)=4i² | |
| |x| | Valeur absolue = distance à 0 | |3|=3 et |-3|=3 car la dist(3,0)=dist(-3,0)=3 | |
| Σ | Symbole se lit « sigma » et correspond à une somme | ||
| σ | Sigma minuscule. Correspond à l’écart-type | σ(1,2,3)=racine(2/3) | |
| ≡ | Congru | S’utilise quand deux nombres ont le même reste dans une division euclidienne 25≡53[7] et se lit « 25=53 modulo 7 » car 25/7 donne un reste de 4 53/7 donne un reste de 4 25 et 53 ont le même reste dans une division par 7 | |
| ! | Factorielle. | Permet de réalisation le produit des entiers de 1 à n Exemple: 3! = 1*2*3=6 Exemple: 5! = 1*2*3*4*5=120 |
J’espère que cet article vous a plu. Dans le même genre, je vous conseille de lire l’article « consignes mathématiques » . Si vous avez une question ou si vous avez rencontré un autre symbole mathématique non mentionné précédemment et que vous ne comprenez pas, n’hésitez pas à m’envoyer un message ci-dessous, je vous répondrai avec plaisir 😊
