De nombreux problèmes mathématiques font intervenir la consigne « montrer que ».
Exemple: Montrer que (x-2)²-4 = x(x-4)
Ce type de consigne est un vrai cadeau, car elle permet aux élèves de savoir quel doit être le résultat à obtenir, et si leur résultat est bon ou pas. Mais cette consigne est souvent « mal » abordée par les élèves. Beaucoup d’élèves ont tendance à écrire :
(x-2)²-4=x(x-4)
⇔ x²-4x+4-4=x²-4
⇔x²-4x=x²-4x
x²-4x=x²-4x donc (x-2)²-4=x(x-4)
✔️ Techniquement, le raisonnement est bon. Mais il nécessite de maîtriser le principe d’équivalence, notion qui n’a rien d’évidente au collège. En effet, à la première ligne, on n’a pas écrit que (x-2)²-4=x(x-4). On a écrit que la proposition (x-2)²-4=x(x-4) est équivalente à x²-4x=x²-4x ce qui est vrai. La conclusion étant vraie, alors la prémisse (première ligne) est vraie. Mais si vous oubliez d’écrire le symbole ⇔ ou la conclusion, le raisonnement tombe à plat et vous n’aurez aucun point sur le raisonnement.
💪 La rédaction par équivalence étant difficile, je vous la déconseille. A la place, je vous conseille plutôt l’une des 3 stratégies suivantes :
Comment montrer que A=B?
Voici les trois techniques les plus utilisées pour montrer une égalité :
| 1. Transformer A → B | 2. Transformer B → A | 3. Transformer A →C & B→C |
| On transforme l’expression de gauche pour aboutir à celle de droite | On transforme l’expression de droite pour aboutir à celle de gauche | On transforme chacun des membres (A et B) pour aboutir à une troisième forme (C) commune |
| Exemple: Montrer que (x-2)²-4 = x(x-4) (x-2)²-4= (x-2)²-2²= (x-2-2)(x-2+2) (x-4)(x) x(x-4) Donc (x-2)²-4 = x(x-4) | Exemple: Montrer que x²+5x+6=(x+2)(x+3) (x+2)(x+3)= x²+3x+2x+6= x²+5x+6 Donc x²+5x+6=(x+2)(x+3) | Exemple: Montrer que (x-2)²-4 = x(x-4) D’une part (x-2)²-4= x²-4x-4+4= x²-4x D’autre part: x(x-4)=x²-4x Donc (x-2)²-4=x(x-4) |
Quelle stratégie adopter?
La stratégie à suivre dépendra du contexte de l’énoncé et des stratégies qui vous semblent le plus simple à mettre en oeuvre. Par exemple si on vous demande
Montrer que (x-3)²-4 = (x-5)(x-1)
Vous pouvez tenter la stratégie n°1, en factorisant l’expression de gauche grâce à l’identité remarquable a²-b²=(a-b)(a+b), ou tenter la stratégie n°3 en développant le membre de gauche, puis le membre de droite. Vous ne savez pas laquelle? Testez…
Technique avancée: Montrer que A-B=0
Pour montrer que A-B=0, vous pouvez également calculer la différence entre les deux membres et montrer que A-B=0
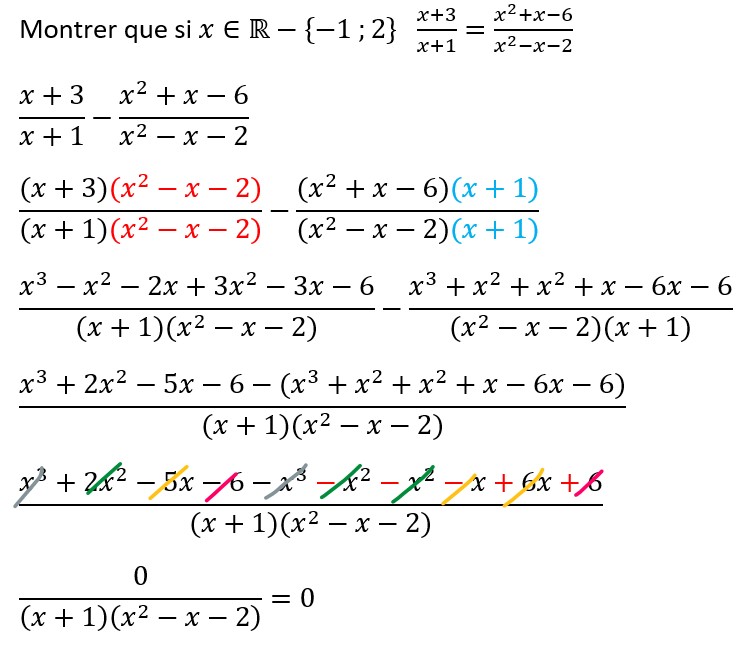
J’espère que cet article vous a été utile, et bonne journée à vous 👋
