Démonstration: (a+b)²=a²+2ab+b²

Depuis la troisième, votre professeur(e) vous serine sans doute que (a+b)²=a²+2ab+b² et qu’il ne faut pas oublier le 2ab quand vous développez un calcul. Ainsi :

Il est facile de vérifier la propriété avec un exemple. Ainsi:

Comme vous le voyez, pour vérifier un calcul en mathématiques, il faut souvent associer plusieurs concepts entre eux. Ici, on peut vérifier l’identité remarquable en se rappelant de la priorité des calculs (parenthèse puis puissance). Mais l’exemple ne fait pas la preuve, alors comment démontrer que (a+b)²=a²+2ab+b² ? C’est ce que nous allons voir maintenant. Avant cela, voici quelques rappels indispensables:

• Si A=B et A=C, alors B=C (en mathématiques, on peut souvent faire des déductions en combinant deux infos différentes d’un même membre, ici a)
• Aire d’un rectangle = Longueur × Largeur.
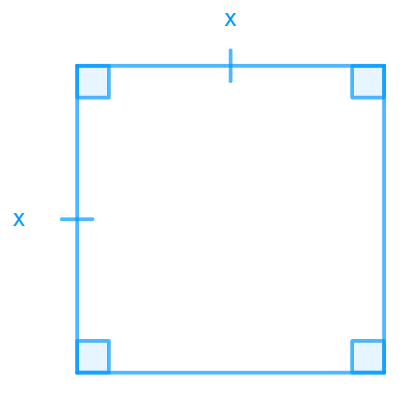
• Dans un carré, Largeur = Longueur d’où Aire = côté ×  côté = côté² (ceci explique d’ailleurs pourquoi la puissance 2 se dit « au carré »).

La démonstration: (a+b)²=a²+2ab+b²

Considérons~une~maison~carrée~divisée~par~deux~murs,~formant~des~pièces~de~dimensions~a~et~b.

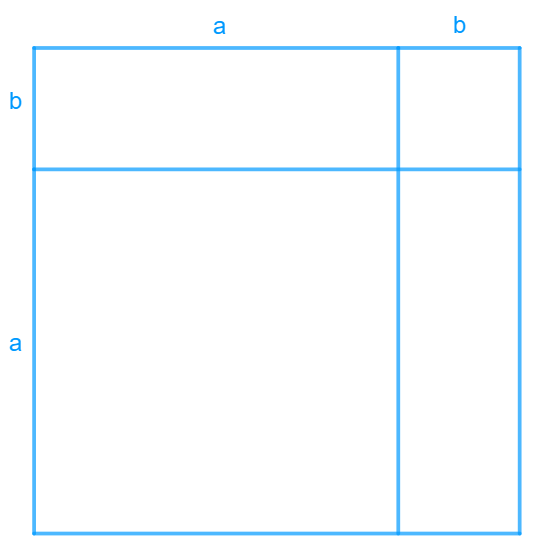
D'après~la~formule~de~l'aire~du~carré:
\\Aire = côté^2=(a+b)^2
\\~
\\~Par~ailleurs,~la~"maison"~est~formée~de~4~pièces.

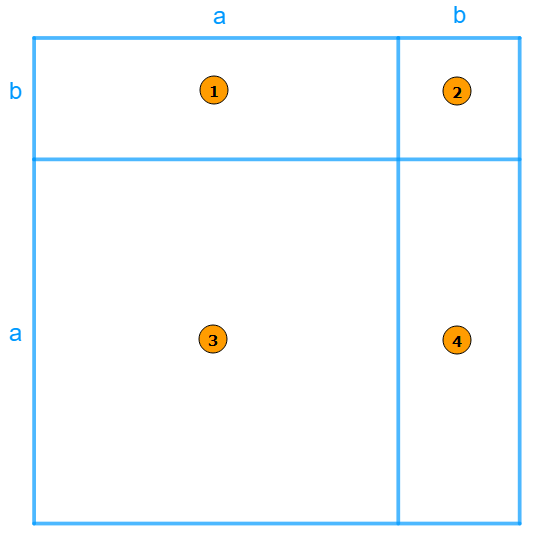
\\~Aire_{maison}=(Aire_{pièce~1})+(Aire_{pièce~2})+(Aire_{pièce~3})+(Aire_{pièce~4})
\\~⇔Aire_{maison}=(a×b)+(b×b)+(a×a)+(b×a)
\\~
\\~Les~pièces~1~et~4~ont~la~même~aire,~donc~Aire_{pièce~1}+Aire_{pièce~4}=2Aire_{pièce~1}=2ab
\\~
\\~⇔Aire_{maison}=a^2+2ab+b^2
\\~
\\~Résumons:
\\~
\begin{cases}
~Aire_{maison}=(a+b)^2 \\
Aire_{maison}=a^2+2ab+b^2
\end{cases}
\\~
\\~En~combinant~les~deux~informations,~on~en~déduit~que~(a+b)^2=a^2+2ab+b²

Le mot de la fin

La démonstration est désormais terminée. Comme vous le voyez, elle n’est pas très compliquée à comprendre à l’aide d’un dessin.

Pour cette raison, de façon générale en mathématiques, quand vous bloquez sur un problème, faites un dessin. Représenter et visualiser aide souvent à venir à bout de problèmes abstraits. Enfin, pensez à combiner les informations. Ici c’est en calculant l’aire de deux manières différentes (côté² ou la somme des pièces) que nous sommes parvenus à démontrer l’identité remarquable. Bonne visite à vous sur BossdesMaths.com 🎓