En seconde, il existe une formule importante au programme qui affirme que pour tous réels a et b > 0, on a: √(a+b)<√a+√b.
Exemple:~si~a=36~et~b=64
\\~
\\\sqrt{36+64}=\sqrt{100}=10~~~~~~~~et~~~~~~~~\sqrt{36}+\sqrt{64}=6+8=14
\\~
\\~10<14
\\~
\\~a=36~et~b=64⇒~\sqrt{a+b}<\sqrt{a}+\sqrt{b}Mais l’exemple ne fait pas la démonstration. Comment vérifier que la formule √(a+b)<√a+√b est vraie pour tous réels a et b > 0 (et pas seulement avec a=36 et b=64)? C’est ce que nous allons voir maintenant :
La stratégie
Pour montrer que A<B, nous allons montrer que A²<B². En effet A²<B²⇔A<B (lorsque A et B sont positifs)
Preuve: Par définition, les racines carrées sont strictement positives (on est bien dans le cas de figure précédemment indiqué). Or, pour x>0, f(x)=x² est croissante, donc la fonction carré conserve l’ordre, c’est-à-dire que si a<b ⇔ f(a)<f(b) c’est à dire a<b⇔a²<b² ou a²<b²⇔a<b (voir graphique ci-dessous) :
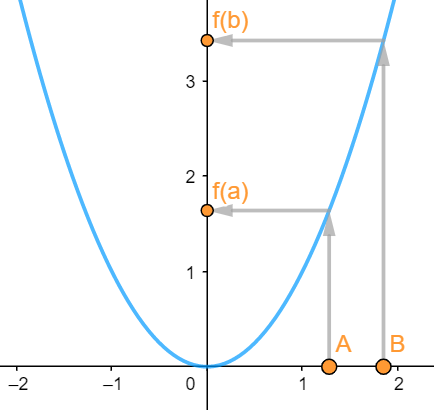
C’est bon? Alors c’est parti 🚀
La démonstration
Nous allons montrer que (√(a+b))²<(√a+√b)² en calculant ce que chacun des membres vaut :
D’une part (membre de gauche) :
~(\sqrt{{\color{orange}a+b}})^2={\color{blue} a+b}
\\~En~effet,~le~carré~annule~la~racine~(rappel:~si~A>0,~\sqrt{{\color{orange}A}}^2={\color{blue}A})D’autre part (membre de droite):
(\sqrt{{\color {blue}a}}+\sqrt{{\color {orange}b}})^2=(\sqrt{{\color {blue}a}})^2+2(\sqrt{{\color {blue}a}})(\sqrt{{\color {orange}b}})+(\sqrt{{\color {orange}b}})^2={\color{blue}a}+{\color{orange}b}+2(\sqrt{{\color {blue}a}})(\sqrt{{\color {orange}b}})=a+b+2\sqrt{ab}En effet :
~({\color {blue}a}+{\color {orange}b})^2={\color {blue}a}^2+2{\color {blue}a}{\color {orange}b}+{\color {orange}b}^2.
\\~Par~ailleurs,~le~carré~annule~une~racine~(rappel:~si~A>0,~\sqrt{{\color{blue}A}}^2={\color{blue}A})Dernière étape (on compare les deux membres)
\\0<2\sqrt{ab}~car~une~racine~est~toujours~positive
\\~
\\0<2\sqrt{ab}
\\⇔{\color{orange}a+b}<{\color{orange}a+b}+2\sqrt{ab}
\\~
\\~Par~ailleurs:
\\{\color{red}a+b}<{\color{green}a+b+2\sqrt{ab}}
\\⇔{\color{red}(\sqrt{a+b})^2}<{\color{green}(\sqrt{a}+\sqrt{b})^2}
\\~
\\En~effet: {\color{red}a+b} = {\color{red}(\sqrt{a+b})^2}~~~~~et~~~~~{\color{green}a+b+2\sqrt{ab}}={\color{green}(\sqrt{a}+\sqrt{b})^2}
\\~
\\(\sqrt{a+b})^2<(\sqrt{a}+\sqrt{b})^2
\\⇔(\sqrt{a+b})<(\sqrt{a}+\sqrt{b})Conclusion
La démonstration est terminée: pour tous réels a et b > 0, on a: √(a+b)<√a+√b. Si cette formule n’est pas très utilisée, elle permet néanmoins de démontrer que √(a+b)≠√a+√b, erreur souvent faite par les élèves en confusion avec la formule √(a×b)=√a×√b (voir fiche « puissances et racines »). Par ailleurs, elle permet de vous familiariser avec la notion de racines, notion qui sera très importante dans la suite de vos études. 💪
Cet article est désormais terminé. J’espère qu’il vous a plu et bonne visite sur BossdesMaths.com
