En sciences, de nombreux phénomènes sont de nature géométriques. Prenons l’exemple des cellules. Les cellules se reproduisent par méiose, c’est-à-dire qu’une cellule se divise en deux. Chaque nouvelle cellule se divisera à son tour en deux nouvelles cellules, et ainsi de suite. Au final, la méiose permet au début de créer 1 nouvelle cellule, puis 2, puis 4, puis 8… Si l’on cherche par exemple à étudier la croissance d’un organisme, on peut être amené se demander: au bout de n méioses, combien de nouvelles cellules ont été créées?
| Nombre de méioses | Nombre de cellules créées | Formule |
| Au bout de 1 méiose | 1 | 1 |
| Au bout de 2 méioses | 3 | 1+2 ou 1+21 |
| Au bout de 3 méioses | 7 | 1+2+4 ou 1+21+22 |
| Au bout de 4 méioses | 15 | 1+2+4+8 ou 1+21+22+23 |
| … | … | … |
| Au bout de n méioses | ??? | 1+21+22+23+…+2n-1 |
Vous le comprenez: ici, pour étudier la croissance cellulaire, vous devez calculer la somme d’une suite géométrique: 1+2+4+8…=1+21+22+23+…+2n. Si n est petit (n=2 ou n=3), le calcul est aisé, mais lorsque n devient grand (exemple: n=10 ou n=20 méioses) vous n’avez pas forcément envie de faire 10 ou 20 additions successives. Pour éviter les calculs redondants et fastidieux, il existe une formule qui permet de gagner du temps, la voici :
Pour~tout~n∈ℕ:~~~~1+q+q^2+...+q^n=\frac{1-q^{n+1}}{1-q}
\\~
\\(si~q≠1,~sinon,~le~dénominateur~vaudrait~0;~ce~qui~n'est~pas~possible,~car~on~ne~peut~pas~diviser~par~0).
Dans notre exemple précédent (méiose), q=2 (le rythme double d’une méiose à la suivante). Au bout de 10 méioses par exemple (n=10), le nombre total de cellules crées sera de:
1+2+2^2+...+2^{\color{orange}9}=\frac{1-2^{9+1}}{1-2}=\frac{1-2^{10}}{-1}=\frac{-1023}{-1}=1023Pratique 😃. Mais comment vérifier que la formule est juste? Vous pouvez vérifier la formule à la main:
1+2+22+23+24+25+26+27+28+29=1+2+4+8+16+32+64+128+256+512 = 1023
Mais cela « tue » le bénéfice de la formule, dont le but premier est de gagner du temps. Et l’exemple ne fait pas la démonstration 😔 Pour nous assurer que la formule est vraie tout le temps, nous allons plutôt le démontrer grâce à l’algèbre 👍
La démonstration
Calculons~(1+q+q^2+q^3+...+q^n)(1-q)
Si l’on développe
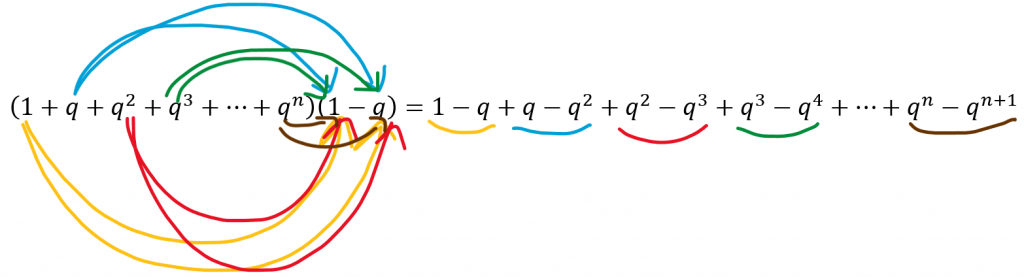
On a donc
\\~(1+q+q^2+q^3+...+q^n)(1-q)=1-q+q-q^2+q^2-q^3+q^3-q^4+...+q^n-q^{n+1}On constate que les termes peuvent se simplifier 2: q avec -q, q² avec -q² etc (voir ci-dessous) :
\\~(1+q+q^2+q^3+...+q^n)(1-q)=1{\color{red}\sout{-q+q}}-{\color{blue}\sout{q^2+q^2}}-{\color{pink}\sout{q^3+q^3}}-q^4+...+q^n-q^{n+1}Il ne reste dès lors que le premier terme et le dernier terme. En effet, outre les simplications précédemment indiquées, on peut aussi éliminer -q4 et qn. Pouquoi? Après -q2 il y a q2, après -q3 il y a q3. Donc après -q4 il y a q4 (que l’on n’avait pas écrit et qui figurait dans les trois petits points). De la même manière, avant qn se trouve -qn. Faisons apparaître ces termes
\\~(1+q+q^2+q^3+...+q^n)(1-q)=1-q+q-q^2+q^2-q^3+q^3-q^4{\color {orange}+~q^4}+...{\color {orange}~-q^n} +q^n-q^{n+1}
En simplifiant les termes
\\~(1+q+q^2+q^3+...+q^n)(1-q)=1{\color{red}\sout{-q+q}}{\color{blue}\sout{-q^2+q^2}}{\color{pink}\sout{-q^3+q^3}}{\color{orange}\sout{-q^4+q^4}}+...+{\color{orange}\sout{-q^n+q^n}}-q^{n+1}Nous avons donc :
(1+q+q^2+q^3+...+q^n)(1-q)=1-q^{n+1}En divisant de chaque côté par 1-q (si q≠1, car si q=1, cela reviendrait à diviser par 0, ce qui est impossible) :
\frac{(1+q+q^2+q^3+...+q^n)(1-q)}{{\color{orange}(1-q)}}=\frac{1-q^{n+1}}{{\color{orange}(1-q)}}
\\~
\\~\frac{(1+q+q^2+q^3+...+q^n){\color{red}\sout{(1-q)}}}{\color{red}\sout{(1-q)}}=\frac{1-q^{n+1}}{1-q}
\\~
\\~1+q+q^2+...+q^n=\frac{1-q^{n+1}}{1-q}
On retombe bien sur la formule souhaitée. 😊 La formule est démontrée. J’espère que la démonstration vous a plu et bonne visite sur Bossdesmaths.com
