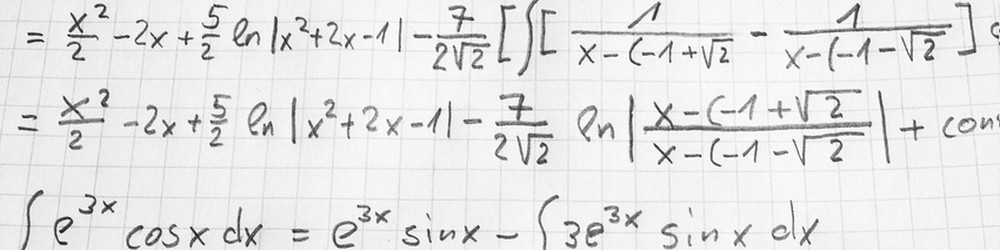Vous avez quelques difficultés à comprendre les maths ? Boss des Maths vous explique les principaux termes mathématiques à maîtriser pour aborder le baccalauréat sereinement.
Termes mathématiques
∀ : Ce symbole signifie « pour tout »
∈ : Ce symbole signifie appartient
∉ : Ce symbole signifie n’appartient pas
Δ : Permet de calculer le discriminant d’une fonction du second degré. Pour le calculer, il faut faire
Δ = b²-4ac. 3 cas de figure sont possibles
Ensemble ℝ (réels) |
Ensemble ℂ (complexes) |
|
Δ > 0 |
||
Δ = 0 |
-b/2a |
|
Δ < 0 |
Pas de solution | |
SSI : Ce terme signifie « SI et seulement SI » et implique une double contrainte au contraire de SI (simple contrainte). Exemple
- S’il pleut, j’irai au cinéma (Rien ne dit que s’il fait beau, je n’irai pas au cinéma)
- Si et seulement s’il pleut, j’irai au cinéma (Je n’irai au cinéma que s’il pleut).
f'(x) désigne la dérivée de la fonction. La dérivée est utile pour connaître la variation d’une fonction. Si f’>0, f est croissante. Si f’<0, f est décroissante. Si f’=0, f est stable. Exemple dans la vie réelle : soit C(x) la courbe du chômage. Si f’>0, le chômage augmente.
f’’(x) ésigne la dérivée seconde. La dérivée seconde sert à étudier la convexité d’une fonction. Si f’’≥0, la fonction est convexe. Si f’’≤0, la fonction est concave. Les points d’inflexion sont faciles à calculer. Ils se situent quand f’’=0
Pour calculer la dérivée seconde, il faut calculer la dérivée (f’) puis dériver une nouvelle fois la fonction.
| Exemple :
f(x) = x3 +3x² f’(x) = 3x² + 6x f’’(x) = 6x + 6 f’’>0 ⇔ 6x+6>0 ⇔ x>-1 f’’<0 ⇔ 6x+6<0 ⇔ x<-1 f’’ = 0 ⇔ 6x+6 =0 ⇔ x=-1 Conclusion : f est convexe entre ]-∞,-1] et concave entre [1,+∞[. Le point d’inflexion est -1. |
F(x) désigne une des primitives de la fonction f(x). Elle sert à calculer une intégrale. La primitive sert à calculer l’aire située entre l’axe des abscisses et la courbe. Dans le monde économique, la primitive sert par exemple à calculer le PIB (richesse d’un pays) en fonction de la courbe de production.

A ∩ B : Signifie l’intersection de l’ensemble A et B (A et B). Exemple : si p(A) désigne la probabilité d’aller à la piscine ce week-end et p(B) celle d’aller au cinéma ce week-end, p(A ∩ B) désigne la probabilité d’aller à la fois au cinéma et à la piscine ce week-end.
A U B : Désigne la probabilité de A ou de B. Dans notre exemple, cela signifie « aller à la piscine OU au cinéma ce weekend ». P(A U B) = P(A)+P(B) – P(A ∩ B )
Ā: Ā désigne l’évènement contraire. Exemple : si p(F) désigne la probabilité pour une femme enceinte d’accoucher d’une fille, p( F barre) désigne la probabilité d’avoir un garçon.
Ensembles : L’ensemble ℕ désigne les entiers naturels (0,1,2,3…). L’ensemble ℤ désigne les entiers relatifs (…, -2,-1,0,1,2,3,…). ℚ désigne l’ensemble des nombres rationnel, c’est à dire les nombres qu’on peut écrire sous forme d’une fraction. Exemple (-5 ; 3/2 ; -1/7 ; 4…). ℝ désigne l’ensemble des nombres réels. Exemple : (-8, , √2, π…). ℂ désigne l’ensemble des nombres complexes. Exemple (-8, , √2, π, 3i, , …)
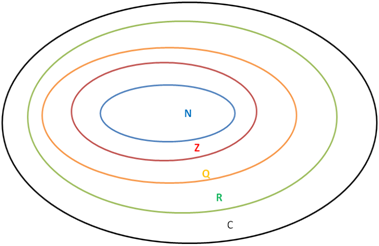
Ensemble étoilé : L’étoile signifie privé de 0. Exemple ℝ* signifie l’ensemble des réels à l’exception de 0.
Ensemble (autre) : + désigne l’ensemble des positifs. Exemple ℝ+ désigne l’ensemble des réels positifs. ℝ- désigne l’ensemble des réels négatifs. L’accolade signifie « privé de ». Exemple : ℝ-{2;4} signifie l’ensemble des réels à l’exception de 2 et de 4. ℕ-{1} signifie l’ensemble des entiers naturels à l’exception de 1.
Coefficient directeur : Le coefficient directeur permet de calculer l’inclinaison de la droite en un point donné. Si le coefficient directeur est positif, la courbe est croissante ; si le coefficient directeur est négatif, la courbe est décroissante. Pour le calculer, il faut calculer la dérivée au point a

Tangente : c’est une droite qui touche la courbe en un point sans la traverser (effleure). Exemple dans la vie réelle : quand on regarde à l’horizon au bord de la mer, la droite portée par le regard est une tangente vis à vis de la courbure de la terre. Soit a ∈ ℝ. La tangente y à la fonction f au point d’abscisse x = a se calcule suivant la formule suivante : y = f’(a)(x-a) + f(a)

Vecteur : Désigne un élément d’un espace vectoriel. Un vecteur est défini par trois choses :
- sa longueur
- son sens (il n’existe que deux sens : exemple : Paris – Lyon, Lyon – Paris)
- sa direction (il en existe une infinité)
Deux vecteurs sont égaux si et seulement si leur longueur, leur sens et leur direction sont les mêmes. Deux vecteurs non nuls sont dits colinéaires si et seulement s’ils ont la même direction.
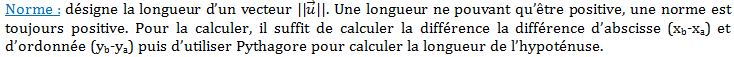
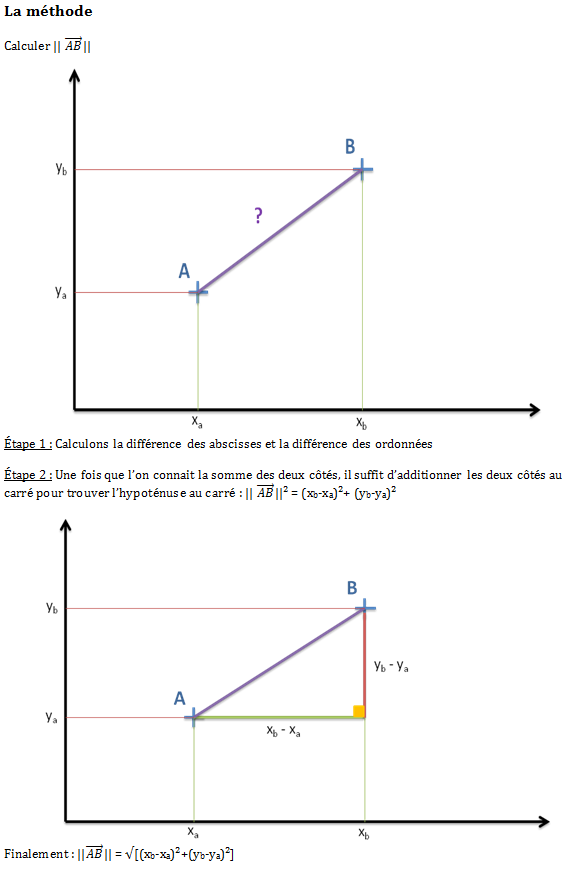
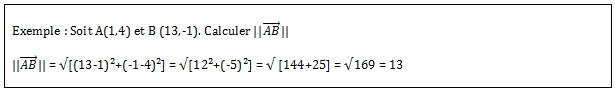
Image et antécédent : l’image désigne l’ordonnée d’une fonction à un endroit donné. L’antécédent désigne l’abscisse d’une fonction à un endroit donné.
Exemple : f(x) = 3x²+2x
Pour x = 2, f(2) = 3×2²+2×2 = 12+4 = 16
Pour x = 2, f(2) = 16
16 est l’image de 2.
2 est un antécédent de 16
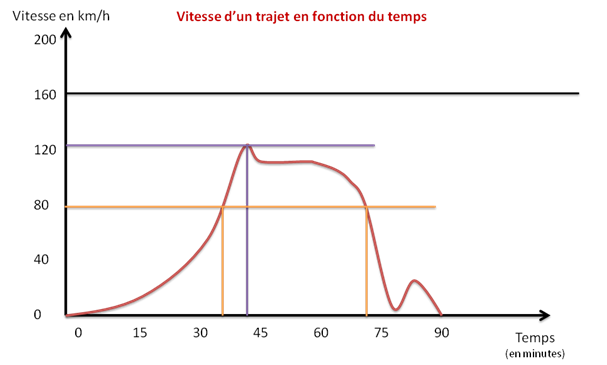
Important : Un point ne peut avoir qu’une image (ex vie réelle : en voiture, à un instant donné, on ne peut aller qu’à une seule vitesse en même temps : on ne peut circuler à 100 km/h et à 120 km/h au même moment). Une image peut avoir plusieurs antécédents (on roule a 80 km/h à la minute 35 et à la minute 70), un seul antécédent (le seul moment où on roule à 120 km/h est la minute 40) ou zéro (160 km/h n’a aucun antécédent : à aucun moment dans un trajet en voiture on a roulé à 160 km/h).
Savoir lire un graphique :
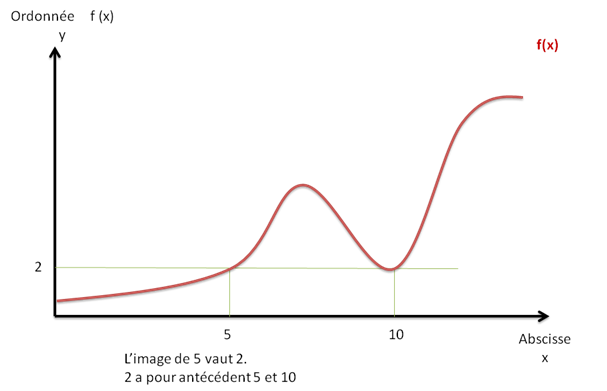
Fonction linéaire : se dit d’une fonction de type f(x) = ax (a∈ℝ) C’est une droite qui passe par l’axe des origines. Cela correspond à une situation de proportionnalité (exemple : prix payé au restaurant en fonction du nombre de convives si chaque personne commande la même chose).
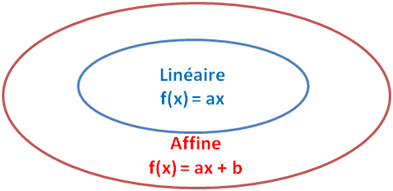
Fonction affine : se dit d’une fonction de type f(x) = ax+b (a,b∈ℝ²). Graphiquement, cela correspond a une droite. Une fonction linéaire est une fonction affine. Par contre l’inverse n’est pas nécessairement vrai (tout comme un carré est un rectangle mais l’inverse n’est pas vrai). Voir schéma ci-dessous.
En savoir plus
Cet article est désormais terminé. J’espère qu’il vous a plu et vous aidera à mieux comprendre les maths. Si vous avez des questions, souhaitez bénéficier de cours particuliers ou participer à l’un des stages Boss des Maths, n’hésitez pas à nous contacter en utilisant le formulaire ci-dessous. Bonne journée à vous et bonnes révisions !