Dans cet article, vous avez découvert pourquoi, dans le cadre d’un cercle trigonométrique de rayon r=1, la formule cos²(x)+sin²(x)=1 est vraie pour tout x∊ℝ. Mais vous pouvez légitimement vous demander: la formule ne fonctionne-t-elle que si r=1? Que se passerait-il si r≠1? Est-ce un paramètre important?
😄 Bonne nouvelle: Peu importe r, la formule cos²(x)+sin²(x)=1 est toujours vraie. La preuve.
Démonstration
Soit~C~un~cercle~trigonométrique~de~centre~O~et~de~rayon~r=k~(avec~k>0) \\Soit~M~un~point~de~C. \\Soit~H~le~pied~de~la~hauteur~issue~de~M.
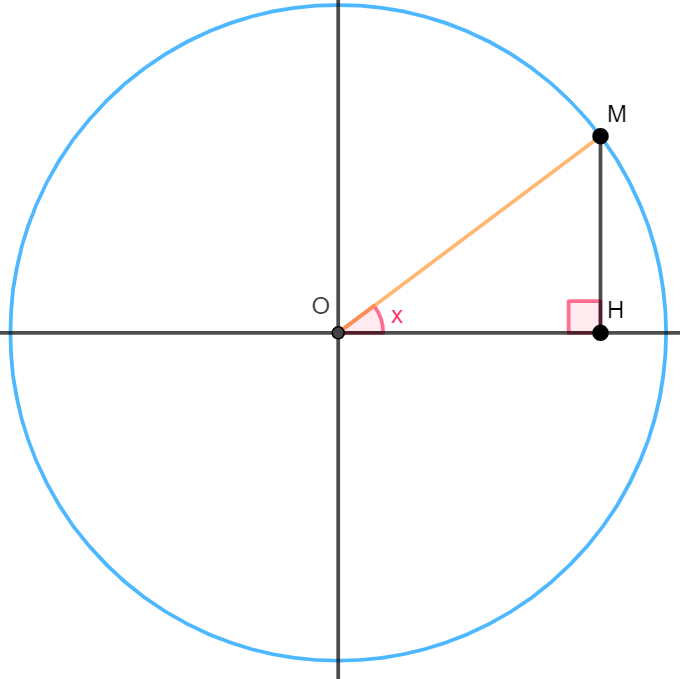
Le~triangle~OMH~est~rectangle~en~H.~D'après~le~théorème~de~Pythagore:
\\OH^2+HM^2=OM^2~⇔~OH^2+HM^2=k^2
\\~
\\Par~ailleurs: cos(x)=\frac{adjacent}{hypoténuse}=\frac{OH}{OM}=\frac{OH}{k}
\\~
\\En~faisant~un~produit~en~croix:~cos(x)=\frac{OH}{k}~⇔~{\color{blue}kcos(x)}={\color{blue}OH}
\\~
\\De~même,~sin(x)=\frac{opposé}{hypoténuse}=\frac{HM}{OM}=\frac{HM}{k}~⇔~{\color{orange}ksin(x)}={\color{orange}HM}
\\~
\\Retournons~à~l'équation~donnée~par~le~théorème~de~Pythagore:
\\~
\\⇔OH^2+HM^2=k^2
\\⇔({\color{blue}OH})^2+({\color{orange}HM})^2=(k)^2
\\⇔({\color{blue}kcos(x)})^2+({\color{orange}ksin(x)})^2=(k)^2
\\⇔k^2cos^2(x)+k^2sin^2(x)=k^2
\\~
\\En~factorisant~par~k^2,~on~trouve~:
\\~
\\⇔k^2[cos^2(x)+sin^2(x)]=k^2(1)
\\⇔{\color {red}\sout{k^2}}[cos^2(x)+sin^2(x)]={\color {red}\sout{k^2}}(1)
\\⇔cos^2(x)+sin^2(x)=1
La démonstration est terminée. Comme vous le voyez, pour tout cercle de rayon r=k (avec k>0), la formule cos²(x)+sin²(x)=1 est vérifiée. Et que se passerait-il si k=0 me diriez-vous? Et bien… Il n’y aurait pas de cercle donc le problème ne serait pas posé 😮
🤓 À quoi ça sert? Prenons un gratte-ciel de 100 étages. Pour construire le 100ème étage, il faut un 99ème étage, donc un 98ème étage et ainsi de suite. Si les premiers étages (ceux du bas) sont mal construits, l’édifice sera bancal et risque de s’écrouler… Il faut donc s’assurer que chacun des 99 premiers étages soient bien construits avant de construire le 100ème étage.
En mathématiques et en sciences, c’est la même chose. Il faut comprendre le concept des nombres pour pouvoir faire des additions. Il faut comprendre les additions pour faire des multiplications; les multiplications pour faire des puissances; le principe des puissances pour comprendre le théorème de Pythagore, et le théorème de Pythagore pour comprendre cette démonstration, et ainsi de suite.
Pour pouvoir faire progresser les sciences, il convient de s’assurer que toutes les formules de base sont vraies 100% du temps. Dans le cas contraire, comment pourrait-on s’assurer que les nouvelles découvertes scientifiques soient vraies si celles-ci s’appuient sur des formules non démontrées et potentiellement fausses? 🤔
C’est pour cette raison que les démonstrations en mathématiques sont très importantes. Elles permettent de s’assurer de la véracité des propositions, et de pouvoir construire l’édifice scientifique sur un socle solide. Par ailleurs, elles vous permettent d’entraîner votre esprit logique (tout comme les pompes aident le sportif à rester en forme). Et avoir un esprit logique vous sera indispensable plus tard si vous êtes amené(e) à faire une prépa, des mathématiques de haut niveau, ou de la recherche scientifique.
Cet article est désormais terminé. J’espère qu’il vous a plu et bonne visite sur BossdesMaths.com
