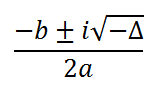Découvrez des stratégies pour préparer le bac de mathématiques

Vous avez envie d’anticiper les révisions du bac en acquérant une solide méthodologie de travail pour bien assimiler votre cours et savoir le mettre en pratique ? Bonne nouvelle : dans cet article, vous découvrirez

Quels sont les 6 moments de l’apprentissage pour progresser durablement
Quelles sont les 4 étapes pour résoudre efficacement un problème mathématique
4 moyens d’analyser vos erreurs pour faire mieux la prochaine fois

Partie I: Les 6 moments de l’apprentissage

Étape n°1 : Lisez votre cours

Cela semble trivial. Néanmoins, connaître votre cours sur le bout des doigts (le programme de terminale, mais aussi les notions vues au cours des années précédentes) est INDISPENSABLE pour résoudre un problème mathématique. D’une part, cela vous évitera de faire des erreurs de calcul. D’autre part, connaître son cours par cœur et réviser régulièrement vous permet de créer des automatismes, donc d’éviter les erreurs de calcul.

Comment faire ? Certaines élèves aiment faire des fiches, d’autres réciter leurs cours à voix haute. Identifiez vos techniques préférées et étudiez par sessions courtes (20-25 minutes), mais intenses (téléphone éteint) et régulières, suivant la méthode de la répétition espacée.

Étape n°2 : Faites des exercices d’application avec votre cours à côté

Connaître votre cours sur le bout des doigts est nécessaire, mais pas suffisant. Vous pouvez connaître votre cours par cœur et avoir 2/20 au prochain DST – si votre copie est bourrée d’erreur de calculs et si vous n’avez pas su mettre en application votre cours… Pour cette raison, ne procrastinez pas et sitôt une notion vue, mettez la en application. Par exemple vous avez appris la formule de dérivée suivante ?

Bam, faites 5 calculs de dérivée de type e^uavec votre cours à côté pour vérifier si vous avez bien utilisé la bonne formule. Le lendemain refaites 1 ou 2 calculs.

À retenir : Il est important de passer rapidement à l’action afin de créer une association entre théorie et pratique, gagner en efficacité et en rapidité. Par ailleurs, ce n’est qu’en faisant de nombreux exercices que vous arriverez à reconnaître les exercices types. Ainsi, le jour du bac, votre cerveau fera inconsciemment l’association entre le sujet en face de vous et les nombreux exercices que vous avez fait, ce qui vous permettra d’identifier facilement une stratégie de résolution.

Certes, faire des exercices d’application n’est pas fun, mais faire des gamme ou des tours de stade non plus. Et ce n’est qu’à ce prix que vous pouvez progresser.

Étape n°3 : Faites des exercices d’application sans votre cours

Une fois que vous êtes à l’aise, refaites les mêmes exercices que ceux de l’étape 2, mais sans votre cours. Une fois que vous êtes à l’aise, augmentez petit à petit la difficulté. Exemple : une fois que vous êtes à l’aise avec les fonctions de type faites quelques exercices avec des fonctions de type e^u puis avec des fonctions de type ke^upuis avec des fonctions de type e^u/v

Objectif: Maintenant que vous connaissez vos formules par cœur, faire des exercices d’application (sans votre cours) renforce vos connexions neuronales et vous permet de gagner en dextérité à l’image d’un sportif qui progresse lentement jour après jour.

Étape n°4 : Faites des problèmes

La principale difficulté des problèmes n’est pas l’aspect mathématique, mais le fait qu’on ne vous dise pas explicitement ce qu’il faut faire. Vous êtes à l’aise avec les exercices d’applications ? Passez aux problèmes. Pour info, la première étape de résolution d’un problème consiste à définir les termes, visualiser la situation et traduire le problème en langage mathématique. Prenons un exemple trivial.

Une piscine parallélépipédique mesure 10 mètres de long, 5 mètres de large et 2 mètres de profondeur. Combien coûte le remplissage, sachant qu’un 1 litre d’eau coûte 0,003€ ?

On veut : Le prix

Comment trouver le prix ? Il faut connaître le volume car volume × prix unitaire = prix total. Comment faire ? Chercher la définition du mot parallélépipédique si nécessaire. Puis calculer le volume :

V = 10×5×2 = 100

Puis

Prix = 100×0,003 = 0,3

On se relit, on se dit que c’est pas logique (0,4€ d’eau pour une piscine) donc on se relit, on identifie une erreur d’inattention (100 = 100m³ , or le prix de l’eau est en litre). Donc on convertit les m³ en litres (100 000 litres), on calcule (100 000×0,003) et on trouve 300€.

Bref, faites de nombreux problèmes. Idéalement :

Faites le problème
Bloqué : relisez votre cours et refaites la question
Bloqué ? Lisez le corrigé et refaites la question. Refaites la à nouveau le lendemain

Etape n°5 : Faites des problèmes type bac

Une fois que vous êtes à l’aise avec les problèmes, avec la démarche scientifique et mathématique, entraînez-vous avec des problèmes type bac (achetez un annabac au besoin, ce n’est pas cher et c’est bien plus pratique que de perdre du temps à chercher des annales sur Internet).

Objectif: comprendre la logique du problème mathématique, arriver à comprendre ce que veux dire le mot « déduire », mener une démarche scientifique et arriver à avancer à tatons même quand vous êtes perdu et arriver à résoudre un problème de plus en plus compliqué type bac. Si jamais vous êtes bloqué au milieu du problème, lisez le corrigé, refaites quelques exercices d’application et refaites à nouveau la question qui vous posait problème.

Etape n°6 : Faites des problèmes en temps limité

Vous êtes désormais (à peu près) à l’aise avec les problèmes ? Faites des problèmes type bac en temps limité, afin d’être mis en condition réelle, de développer votre endurance, votre gestion du temps et votre capacité de concentration.

	Action	But
Étape 1	Apprendre par coeur votre cours	• Maîtriser les bases théoriques et éviter les erreurs de formule
Étape 2	Exercices d’application avec votre cours jusqu’à vous sentir confortable	• Apprendre à déchiffrer les énoncés • Savoir appliquer une formule dans un contexte donné • Découvrir les exercices type
Étape 3	Exercices d’application sans votre cours	• Assimilation du cours • Création d’automatismes • Améliorer vos points faibles • Gain de rapidité
Étape 4	Faire des problèmes	• Améliorer votre méthodologie • Identifier des stratégies de résolution • Améliorer vos capacités d’analyse
Étape 5	Faire des exercices type bac (sans limite de temps)	• Réviser l’ensemble du programme de l’année en contexte • Savoir traiter tous types de problèmes en condition réelle
Étape 6	Problème type bac (en temps limité)	• Apprendre à gérer votre temps • Augmenter votre capacité de concentration • Développer votre endurance

Partie II: Les 4 étapes pour résoudre un problème mathématique

Comme indiqué précédemment, pour progresser en maths, il est important de connaître votre cours et de savoir l’appliquer dans le cadre d’exercices d’application. Mais savoir résoudre un problème est souvent une autre paire de manche. Comment faire ? C’est ce que nous allons voir maintenant.

Étape 1 : Lisez l’énoncé

« Rien ne sert de courir ; il faut partir à point. » (Jean de la Fontaine)

Beaucoup d’élèves cherchent à résoudre un problème au plus vite. C’est une erreur. Prenez le temps de lire attentivement l’énoncé. Définissez les termes (si on vous demande de déterminer les paramètres d’une loi normale et que vous ne savez pas ce que c’est, recherchez ce que veut dire « paramètre »). Faites un schéma ou imaginez un exemple de la vie courante pour visualiser le problème.

Les problèmes suivent toujours une certaine logique, chaque question n’a de sens que prise dans le contexte global du problème. Lisez l’ensemble des questions du problème pour comprendre comment la question s’insère dans le problème.

Étape 2 : Identifiez les infos à votre disposition

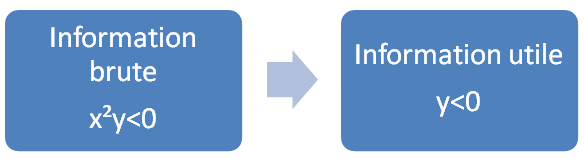
Listez l’ensemble des informations à votre disposition. L’information peut se trouver dans l’énoncé, les questions précédentes ou les questions suivantes. Des informations peuvent être implicites. Pensez à les identifier (exemple : si on vous dit : 80% des élèves ont eu la moyenne, c’est que 20% ne l’ont pas eu). Enfin, l’information brute en temps que telle n’a aucune valeur. Pensez à extraire de l’information utile.

Par exemple, si l’énoncé indique x²y<0, cela signifie que y est négatif car on sait qu’un carré est toujours positif.

Étape 3 : Trouvez le chemin

Maintenant que vous avez listé l’ensemble des informations utiles, demandez-vous lesquelles peuvent vous aider à répondre à la question. Voici quelques pistes de réflexion qui peuvent vous aider :

a. Définissez les termes

Assurez-vous de bien comprendre l’énoncé. « Montrer que » signifie que vous connaissez la réponse finale et qu’il faut juste trouver le raisonnement qui permet de trouver la réponse à partir des questions précédentes ou des éléments de l’énoncé. Faites autant d’essais que nécessaire jusqu’à trouver la solution. On vous dit « en déduire » ? Cela signifie que les réponses précédentes doivent être exploitées pour répondre à la question. Lesquelles ? Cherchez.

Si on vous introduit une nouvelle donnée, c’est sans doute qu’elle est utile. Si vous avez étudié f(x) depuis 3 questions et qu’on vous parle de g(x), c’est sans doute qu’il faut identifier un lien logique entre f(x) et g(x). Même si vous ne voyez pas le lien logique, dites-vous qu’il y a en a toujours un.

b. Jouez la ressemblance

Si on cherche P(X≤a) et que les seules informations dont vous connaissez sont P(X=a) et P(x>a), vous devez arriver à identifier que P(X≤a) ressemble à P(x>a) : ce sont deux inégalités, mais pas dans le même sens. Reste plus qu’à utiliser la formule P(Â) = 1-P(A) pour trouver : P(X≤A) = 1 – P(X>A).

c. Lisez la question suivante.

En effet, les questions des problèmes se suivent suivant une certaine logique, et souvent, la question suivante peut vous donner des indices (voire même la réponse de la question qui vous semble si difficile).

Prenons l’exemple de l’exercice 3 issu du sujet de « math bac S France métropolitaine, juin 2015 »

À la première question, on demande de résoudre l’équation dans ℂ. On reconnaît un polynôme du second degré donc on sait qu’on a forcément deux solutions (sauf si Δ=0) :

• Deux solutions dans ℝ si Δ>0

• Deux solutions dans ℂ dans le cas contraire.

Or regardez à la question 2 : on nous donne arbitrairement l’affixe de 3 points. Comme par hasard, les points a et b font étonnement penser aux racines d’un polynôme que sont

Sans même faire de calcul, vous pouvez vous douter qu’il y a 99% de chance que A et B soient la réponse de la question 1. Evidemment, votre intuition (qui ici s’avère juste) ne vous dispense pas de faire le calcul de la question 1. Mais cela peut vous aider (lorsque vous êtes bloqué à une question) et vous permettre de détecter d’éventuelles erreurs de calcul.

d. Listez l’ensemble des formules et théorèmes

Listez les théorèmes associés à la thématique du problème et demandez-vous quelle formule/théorème semble être les plus utiles pour répondre à la question eu égard aux informations à votre disposition (voir étape 2).

Vous avez identifié plusieurs méthode de résolution ? Vous ne savez pas quelle méthode utiliser ? Testez les une par une pour trouver la meilleure méthode de résoudre le problème.

Étape 4 : Effectuez le calcul

Maintenant que vous avez identifié les informations et formules utiles pour résoudre le problème alors il est temps de résoudre le problème. Enfin, n’oubliez pas de vous relire pour éviter les erreurs d’inattention et de calcul.

Partie III: 4 moyens d’analyser vos erreurs pour faire mieux la prochaine fois

Travailler efficacement et savoir résoudre un problème est bien, mais que faire si vos notes ne décollent pas ? Voici 4 pistes de réflexion qui, je l’espère, vous aideront à progresser.

#1 : Analysez-vous

« Connais-toi toi même » Socrate

Par Sting, CC BY-SA 2.5

Reprenez vos vieux DST et analysez vos erreurs en fonction de leur nature. Par exemple si vous avez eu 10 au dernier DST, peut-être avez-vous perdu les points ainsi

• 1 point : erreur de calcul

• 2,5 points : raisonnement mal rédigé

• 3 points : manque de temps dernier exercice

• 2 points : question non sue

• 1,5 point : confusion formule

Suivant la bonne vieille loi de Pareto:

20% des erreurs les plus fréquentes produisent 80% des pertes de point.

Listez 2-3 items à corriger en priorité, puis notez les sur une check-list et faites de nombreux exercices en retravaillant ces 2-3 items plus particulièrement. Par exemple: vous faites beaucoup d’erreurs de signe? Alors relisez systématiquement les signes (ou notez les dans une autre couleur par exemple) jusqu’à ce que point spécifique ne pose plus de problème.

#2 Refaites vos vieux DST

Ecouter le professeur lors de la correction d’un DST ne suffit pas. En effet, comprendre la logique et le cheminement mental de votre prof ne veut pas dire que vous saurez refaire par vous-même l’exercice. Ecouter la correction est bien sûr indispensable, mais refaites systématiquement chaque DST à la maison une ou deux semaines plus tard. Si vous n’avez pas le temps, faites a minima les exercices où vous vous étiez le plus planté.

#3 Privilégiez les problèmes corrigés

Si vous avez des difficultés en mathématiques, faites en priorité des problèmes corrigés. Si vous bloqués, lisez la réponse et essayez de la trouver par vous-même. Si vous ne trouvez pas, lisez les explications et refaites le problème par vous-même.

#4 : Changez de méthode

Rappel : Résultats = Quantité de travail × Productivité

Si vous travaillez énormément les maths et que les résultats ne suivent pas, peut-être est-ce parce que vos méthode de travail ne sont pas efficaces.

Vous révisez vos cours le soir ? Alors essayez le matin
Vous révisez vos cours avec des fiches ? Pourquoi ne pas essayer de réciter votre cours à haute voie ? De le dessiner ?
Vous révisez vos cours seul chez vous ? Pourquoi ne pas aller à la bibliothèque à la place
Vous n’arrivez pas à vous motiver ? Faites un tableau comme celui ci-dessous et indiquez une croix pour chaque jour où vous travaillez vos maths. Ainsi, cela vous permettra de visualiser vos progrès

	Semaine 1	Semaine 2	Semaine 3
Lundi
Mardi
Mercredi
Jeudi
Vendredi
Samedi

Apprenez à anticiper. Faire un exercice type bac chaque semaine de janvier à la mi-mars revient au même que faire 2 à 3 bacs blancs ! Enfin, n’oubliez pas de vous motiver avec le système de carotte/bâton. Vous avez tenu vos objectifs ? Alors sortez avec des amis, faites du sport ou toute activité qui vous fait plaisir !

Cet article est désormais terminé. J’espère qu’il vous a plu. Si vous avez besoin de conseils ou d’aides en mathématiques, sachez que je donne des cours particuliers et des stages collectifs intensifs en petit groupe. N’hésitez pas à me contacter pour me faire part de vos attentes 🙂

♟️ Stratégie pour améliorer vos notes au Bac